IV. Brüche 3m /2n, die sich der 1 annähern
Niemals kann gelten 3m = 2n für natürliche Zahlen m, n.
Allerdings kann 3m/2n der 1 beliebig nahe kommen, es entstehen „Kommata“.
Um solche m und n zu gewinnen kann man folgende Gleichung auflösen:
3m = 2n
m·log(3) = n·log(2)
m/n = log(2)/log(3)
Die irrationale Zahl log(2)/log(3) = 0,6309297536... kann man durch die Näherungsbrüche ihrer Kettenbruchentwicklung
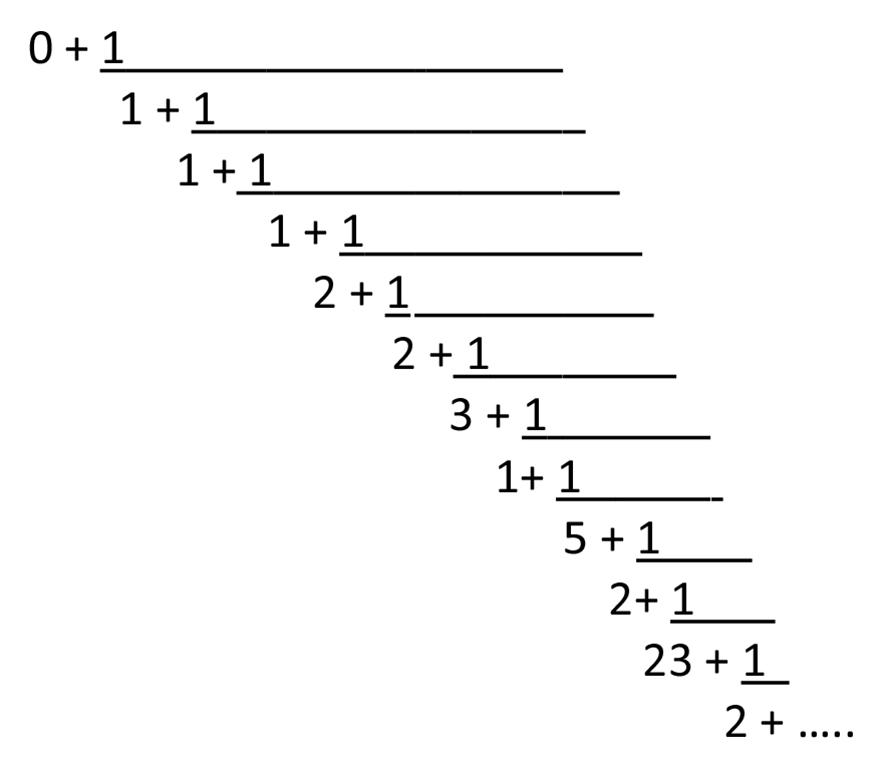
annähern,
das sind
0/1, 1/1, 1/2, 2/3, 5/8, 12/19, 41/65, 53/84, 306/485, 665/1054, 15601/24727, 31867/50508 ......
Man gewinnt dadurch folgende „Kommata“:
| Zahlenverhältnis | Centmaß | |||||
| Oktav-1 | K0 = O-1 = | 1/2 | [O-1] = | - o | = | - 1200,0000000 |
| Quint | K1 = Qui = | 3/2 | [Qui] | = | 701,9550009 | |
| Quart-1 | K2 = Qua-1 = | 3/22 | [Qua-1] | = | - 498,0449991 | |
| Tonus | K3 = T = | 32/23 | [T] = | t | = | 203,9100017 |
| Semitonium-1 | K4 = S-1 = | 35/28 | [S-1] = | - s | = | - 90,2249957 |
| Pythagoräisches Komma | K5 = P = | 312/219 | [P] = | p | = | 23,4600104 |
| K6 = Q = | 341/265 | [Q] = | = | - 19,8449645 | ||
| K7 = R = | 353/284 | [R] = | r | = | 3,6150459 | |
| K8 = U = | 3306/2485 | [U] = | = | - 1,7697352 | ||
| K9 = V = | 3665/21054 | [V] = | = | 0,07557548 | ||
| K10 = W = | 315601/224727 | [W] = | = | - 0,03149909 | ||
| K11 = M = | 331867/250508 | [M] = | = | 0,01257731 |
Es gelten folgende Beziehungen zwischen je drei aufeinanderfolgenden Kommata dieser Reihe:
| O-1·Qui = Qua-1 | [O-1] + [Qui] = [Qua-1]] | |
| Qui· Qua-1 = T | [Qui] + [Qua-1]] = [T] | |
| Qua-1·T2 = S-1 | [Qua-1] + 2·[T] = [S-1] | |
| T·S-2 = P | P [T] + 2·[S-1] = [P] | |
| S-1·P3 = Q | [S-1] + 3·[P] = [Q] | |
| P·Q = R | [P] + [Q] = [R] | |
| Q·R5 = U | [Q] + 5·[R] = [U] | |
| R·U2 = V | [R] + 2·[U] = [V] | |
| U·V23 = W | [U] + 23·[V] = [W] | |
| V·W2 = M | [V] + 2·[W] = [M] |