genus musicum (XXIII.)

 genus musicum (XXIII.)       exponens 2m·33·52·7
   F  Fs*  Fs  G*  G  Gs*  Gs  A*  A  B*  B  H*  H  c*  c  cs*  cs  d*  d  ds*  ds  e*  e  f*  f
 212  23·3·52·7  25·33·5  27·5·7  29·32  20·33·52·7  26·3·52  24·32·5·7  210·5  28·3·7  23·33·52  25·52·7  27·32·5  25·33·7  211·3  22·32·52·7  28·52  26·3·5·7  28·33  210·7  25·32·52  23·33·5·7  29·3·5  27·32·7  213
4096   4200  4320 4480   4608  4725 4800  5040  5120   5376  5400  5600 5760   6048 6144   6300  6400  6720  6912  7168  7200  7560  7680  8064  8192
 f  213   8192  1/2  525/1024  135/256  35/64  9/16 4725/8192  75/128  315/512  5/8  21/32  675/1024  175/256  64/45  189/256  3/4  1575/2048  25/32  105/128  27/32  7/8  225/256  945/1024  15/16  63/64  1
 f*  27·32·7  8064  32/63  25/48  15/28  5/9  4/7  75/128  25/42  5/8  40/63  2/3  75/112  36/25  5/7  4/3  16/21  25/32  50/63  5/6  6/7  8/9  25/28  15/16  20/21  1  64/63
 e  29·3·5  7680  8/15  35/64  9/16  7/12  3/5  315/512  5/8  21/32  2/3  7/10  64/45  35/48  4/3  63/80  4/5  105/128  5/6  7/8  9/10  14/15  15/16  63/64  1  21/20  16/15
 e*  23·33·5·7  7560  512/945  5/9  4/7  16/27  64/105  5/8  40/63  2/3  128/189  32/45  5/7  20/27  16/21  4/5  256/315  5/6  160/189  8/9  32/35  128/135  20/21  1  64/63  16/15  1024/945
 ds  25·32·52  7200  128/225  7/12  3/5  28/45  16/25  21/32  2/3  7/10  32/45  56/75  4/3  7/9  4/5  21/25  64/75  7/8  8/9  14/15  24/25  224/225  1  21/20  16/15  28/25  256/225
 ds*  210·7  7168  4/7  75/128  135/224  5/8  9/14  675/1024  75/112  64/45  5/7  4/3  675/896  25/32  45/56  27/32  6/7  225/256  25/28  15/16  27/28  1  225/224  135/128  15/14  9/8  8/7
 d  28·33  6912  16/27  175/288  5/8  35/54  2/3  175/256  25/36  35/48  27/20  7/9  25/32 175/216  5/6  7/8  8/9  175/192  25/27  35/36  1  28/27  25/24  35/32  10/9  7/6  32/27
 d*  26·3·5·7  6720  64/105  5/8  9/14  2/3  24/35  64/45  5/7  4/3  16/21  4/5  45/56  5/6  6/7  9/10  32/35  15/16  20/21  1  36/35  16/15  15/14  9/8  8/7  6/5  128/105
 cs  28·52  6400  16/25  21/32  27/40  7/10  18/25  189/256  4/3  63/80  4/5  21/25  27/32  7/8  9/10  189/200  24/25  63/64  1  21/20  27/25  28/25  9/8  189/160  6/5  63/50  32/25
 cs*  22·32·52·7  6300  1024/1575  2/3  24/35  45/32  128/175  4/3  16/21  4/5  256/315  64/75  6/7  8/9  32/35  24/25  512/525  1  64/63  16/15  192/175  256/225  8/7  6/5  128/105  32/25  2048/1575
 c  211·3  6144  2/3  175/256  45/64  35/48  4/3  1575/2048  25/32  105/128  5/6  7/8  225/256  175/192  15/16  63/64  1  525/512  25/24  35/32  9/8  7/6  75/64  315/256  5/4  21/16  4/3
 c*  25·33·7  6048  128/189  25/36  5/7  27/20  16/21  25/32  50/63  5/6  160/189  8/9  25/28  25/27  20/21  1  64/63  25/24  200/189  10/9  8/7  32/27  25/21  5/4  80/63  4/3  256/189
 H  27·32·5  5760  32/45  35/48  4/3  7/9  4/5  105/128  5/6  7/8  8/9  14/15  15/16  35/36  1  21/20  16/15  35/32  10/9  7/6  6/5  56/45  5/4  21/16  4/3  7/5  64/45
 H*  25·52·7  5600  128/175  4/3  27/35  4/5  144/175  27/32  6/7  9/10  32/35  24/25  27/28  1  36/35  27/25  192/175  9/8  8/7  6/5  216/175  32/25  9/7  27/20  48/35  36/25  256/175
 B  23·33·52  5400  512/675  7/9  4/5  112/135  64/75  7/8  8/9  14/15  128/135  224/225  1  28/27  16/15  28/25  256/225  7/6  32/27  56/45  32/25  896/675  4/3  5/7  64/45  112/75  1024/675
 B*  28·3·7  5376  16/21  25/32  45/56  5/6  6/7  225/256  25/28  15/16  20/21  1  225/224  25/24  15/14  9/8  8/7  75/64  25/21  5/4  9/7  4/3  75/56  45/32  10/7  3/2  32/21
 A  210·5  5120  4/5  105/128  27/32  7/8  9/10  945/1024  15/16  63/64  1  21/20  135/128  35/32  9/8  189/160  6/5  315/256  5/4  21/16  27/20  5/7  45/32  189/128  2/3  63/40  8/5
 A*  24·32·5·7  5040  256/315  5/6  6/7  8/9  32/35  15/16  20/21  1  64/63  16/15  15/14  10/9  8/7  6/5  128/105  5/4  80/63  4/3  48/35  64/45  10/7  2/3  32/21  5/8  512/315
 Gs  26·3·52  4800  64/75  7/8  9/10  14/15  24/25  63/64  1  21/20  16/15  28/25  9/8  7/6  6/5  63/50  32/25  21/16  4/3  5/7  36/25  112/75  2/3  63/40  5/8  42/25  128/75
 Gs*  20·33·52·7  4725  4096/4725  8/9  32/35  128/135  512/525  1  64/63  16/15  1024/945  256/225  8/7  32/27  128/105  32/25  2048/1575  4/3  256/189  64/45  256/175  1024/675  32/21  5/8  512/315  128/75  8192/4725
 G  29·32  4608  8/9  175/192  15/16  35/36  1  525/512  25/24  35/32  10/9  7/6  75/64  175/144  5/4  21/16  4/3  175/128  25/18  35/24  2/3  14/9  25/16  105/64  5/3  7/4  16/9
 G*  27·5·7  4480  32/35  15/16  27/28  1  36/35  135/128  15/14  9/8 8/7  6/5  135/112  5/4  9/7  27/20  48/35  45/32  10/7  2/3  54/35  5/8  45/28  27/16  12/7  9/5  64/35
 Fs  25·33·5  4320  128/135  35/36  1  28/27  16/15  35/32  10/9  7/6  32/27  56/45  5/4  35/27  4/3  5/7  64/45  35/24  40/27  14/9  5/8  224/135  5/3  7/4  16/9  28/15  256/135
 Fs*  23·3·52·7  4200  512/525  1  36/35  16/15  192/175  9/8  8/7  6/5  128/105  32/25  9/7  4/3  48/35  36/25  256/175  2/3  32/21 5/8  288/175  128/75  12/7  9/5  64/35  48/25  1024/525
 F  212  4096  1  525/512  135/128  35/32  9/8  4725/4096  75/64  315/256  5/4  21/16  675/512  175/128  45/32  189/128  2/3  1575/1024  25/16  105/64  27/16  7/4  225/128  945/512  15/8  63/32  2

Graphische logarithmische Darstellung der Tongeschlechter (XXI.), (XXII.) und (XXIII.):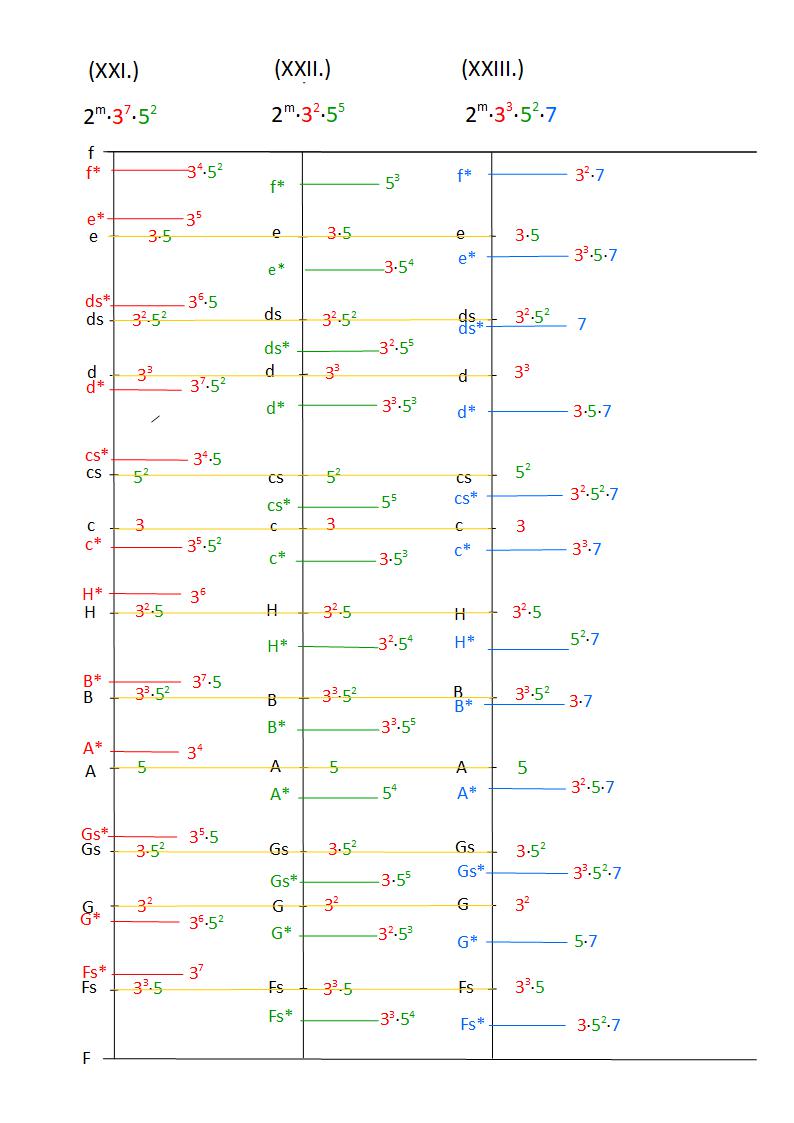
21 23

Im Kapitel über "verschiedene Kommata und Intervalle" auf dieser Homepage habe ich beschrieben, wie die Intervalle 3 (3/2), 5 (5/4) und 7 (7/4) durch 31, 17, bzw. 43 Holder-Kommata (21/53) angenähert werden können. Für alle Töne der oben beschriebenen Tongeschlechter ergeben sich daher - übertragen auf die Grundoktav - folgende Annäherungen durch Holder-Kommata:

 ·  30 31 32  33 
 50  0  31  9  40
 51  17  48  26  4
 52  34  12  43  21

  ·  34 35  36  37 
 50  18  49  27  5
 51  35  13  44  22
 52  52  30  8  39

  ·  30 31  32  33
 53  51  29  7  38
 54  15  46  24  2
 55  32  10  41  19

  ·  30  31  32  33
 50·7  43  21  52  30
 51·7  7  38  16  47
 52·7  24  2  33  11

21 23 Holder

Konsonanzen

Aus den 12 species  von Konsonanzen des "genus diatonico-chromaticum" können in diesem Tongeschleecht noch zusätzliche 12 durch Multiplikation mit dem Faktor 7 gefunden werden:

species I* 2m·7
species II*   2m·3·7
species III*   2m·5·7 
species IV* 2m·32·7
species V*   2m·3·5·7 
species VI*   2m·52·7 
species VII*   2m·33·7
species VIII*   2m·32·5·7 
species IX*   2m·3·52·7
species X*   2m·33·5·7 
species XI*   2m·32·52·7
species XII*   2m·33·52·7

 Für die oben aufgelisteten Konsonanzen ergeben sich folgende "Grade der Annehmlichkeit":
(GS(E) = (Summe aller Primteiler von E) – (Anzahl aller Primteiler von E) + 1)

  gradus suavitatis   VII VIII IX X XI XII XIII XIV XV XVI XVII XVIII XIX XX XXI XXII XXIII
species I* 7 2·7   22·7          
species II* 3·7   2·3·7  22·3·7   23·3·7        
species III* 5·7   2·5·7   22·5·7   23·5·7   24·5·7        
species IV*  32·7    2·32·7  22·32·7   23·32·7   24·32·7        
species V*              3·5·7  2·3·5·7  22·3·5·7 23·3·5·7  24·3·5·7       
species VI*    52·7  2·52·7  22·52·7  23·52·7  24·52·7       
species VII*          33·7 2·33·7  22·33·7  23·33·7   24·33·7       
speciesVIII*    25·32·5 32·5·7 32·5·7   2·32·5·7 22·32·5·7 23·32·5·7  24·32·5·7       
species IX*            3·52·7  2·3·52·7   22·3·52·7   23·3·52·7       
species X*     33·5 ·7 2·33·5·7   22·33·5·7  23·33·5·7       
species XI*   32·52·7 2·32·52·7   22·32·52·7  22·33·52·7  
species XII* 33·52·7 2·33·52 ·7  22·33·52·7

 

Ähnlich wie beim "genus diatonico-chromaticum" können wir diese Konsonanzen in zwei Fünfliniensystemen aufschreiben:
(Als untere Grenze nehmen wir hier das C, als obere das c'".)
• : die 12 Töne aus dem Geschlecht 2m·33·52
• : die 12 durch Multiplikation mit 7 erhaltenen zusätzlichen Töne

species I*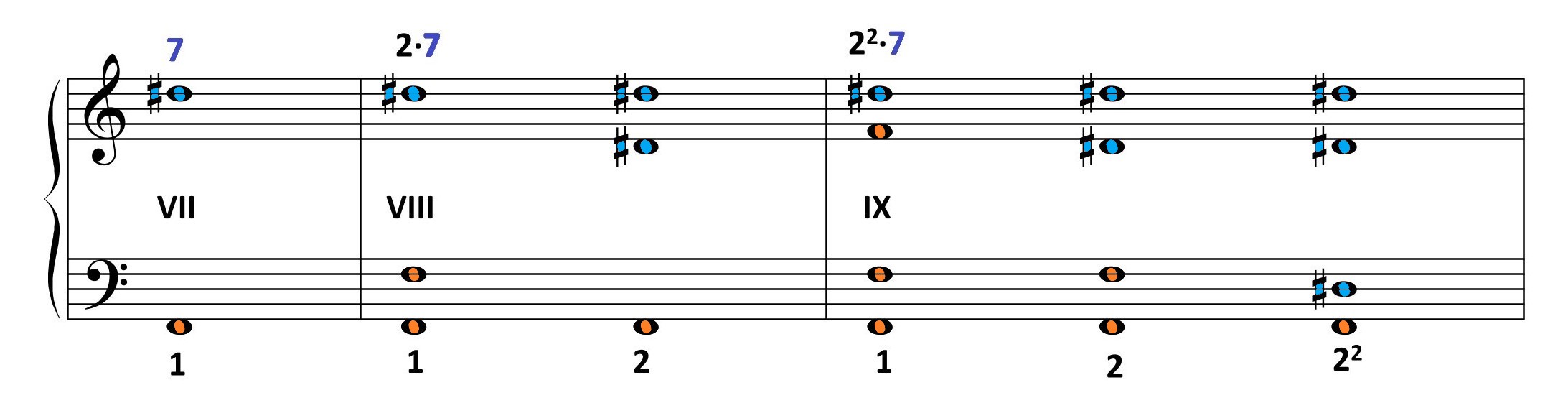
Konsonanzen Homepage species I7

 

7
F=1

  

2·7
F=1

2·7
F=2

  

22·7
F=1

 22·7
F=2		 22·7
F= 22

 

species II*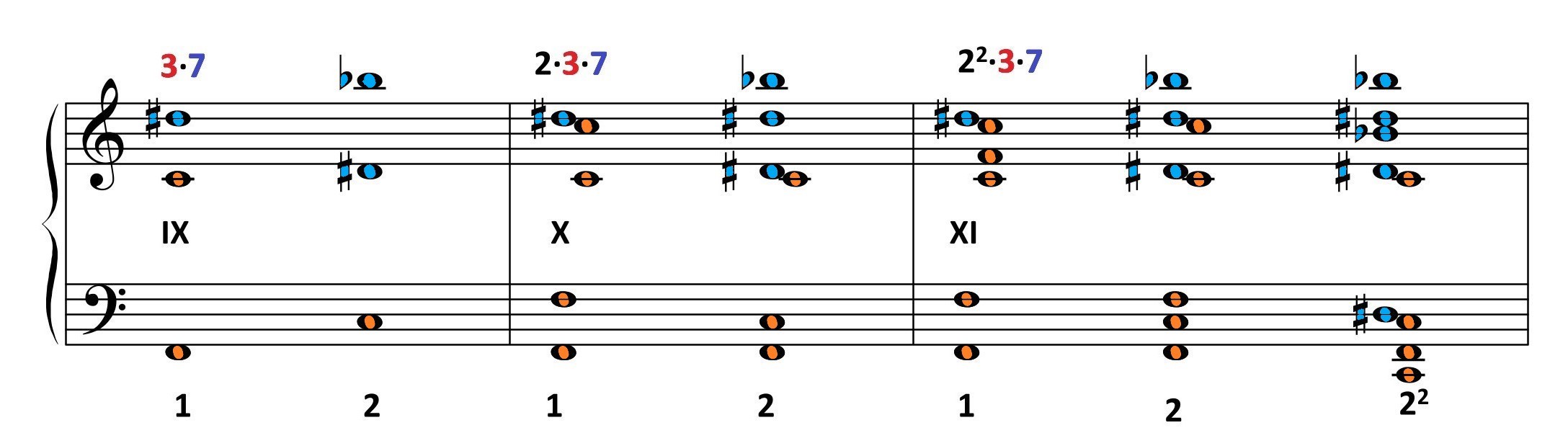
Konsonanzen Homepage species II7

 

3·7
F=1

3·7
F=2

   2·3·7
F=1

2·3·7
F=2

  

22·3·7
F=1

 22·3·7
F=2		 22·3·7
F=22

 

species III*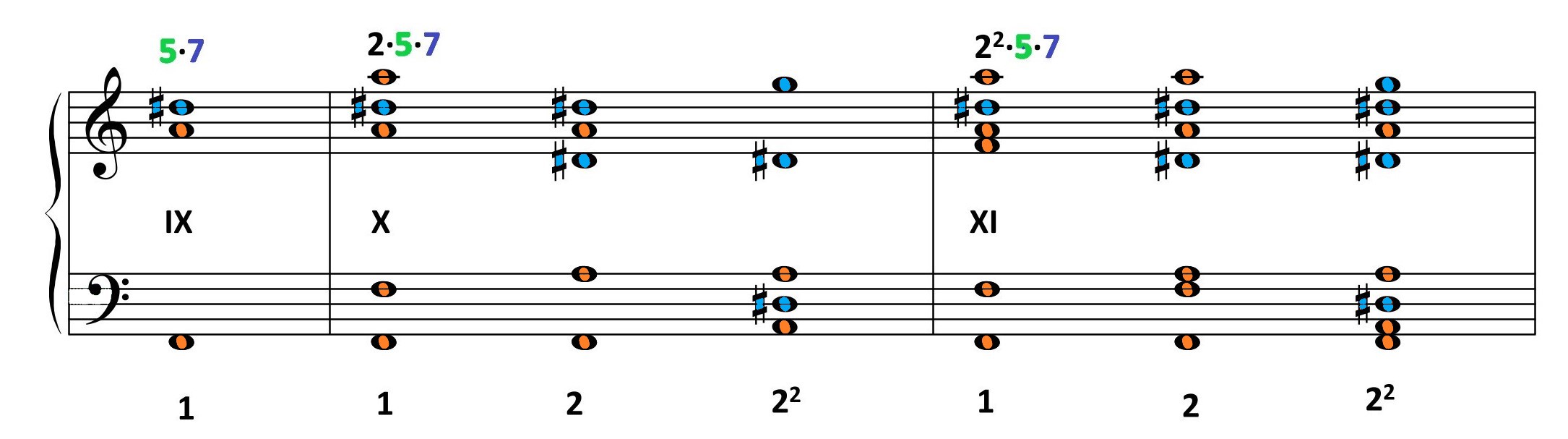
Konsonanzen Homepage species III7

 

5·7
F=1

   2·5·7
F=1		 2·5·7
F=2

2·5·7
F=22

  

22·5·7
F=1

 22·5·7
F=2		 22·5·7
F=22

 

species IV*Konsonanzen Homepage species IV7

  32·7
F=1

32·7
F=2

 32·7
F=22		 32·7
F=23		   2·32·7
F=1		 2·32·7
F=2		 2·32·7
F=22		 2·32·7
F=23


22·32·7
F=1

 22·32·7
F=2		 22·32·7
F=22		 22·32·7
F=23		   23·32·7
F=1		 23·32·7
F=2		 23·32·7
F=22		 23·32·7
F=23
  24·32·7
F=1 		   24·32·7
F=2		   24·32·7
F=22		   24·32·7
F=23		    

 

species V*
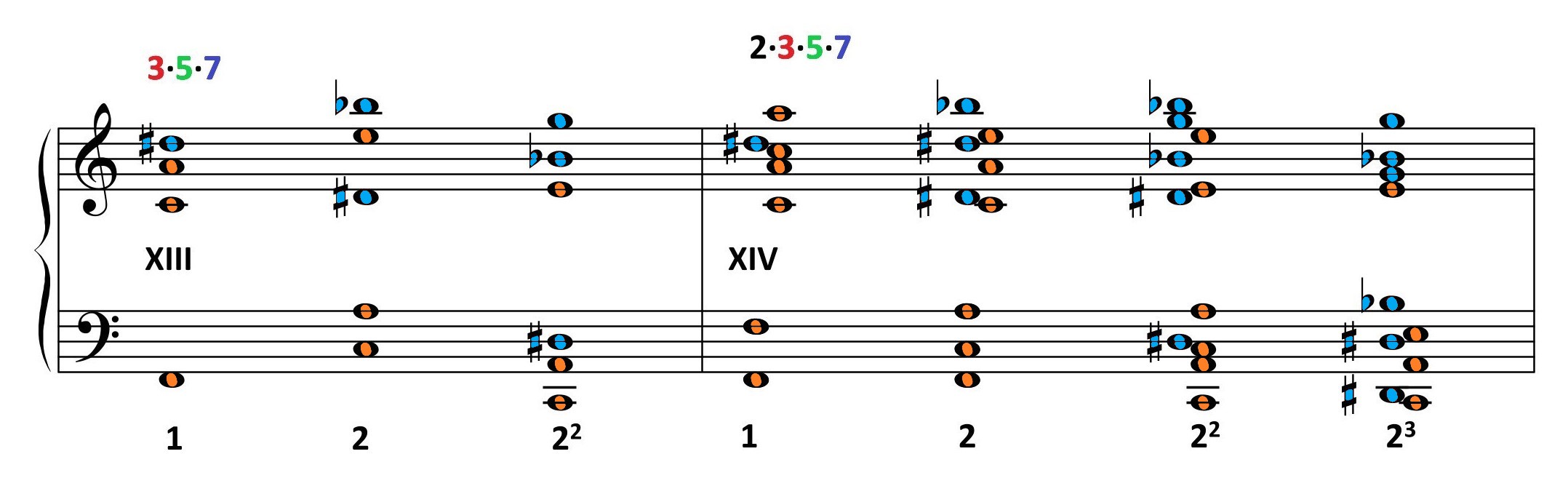
Konsonanzen Homepage species V7Konsonanzen Homepage species V7 2

  3·5·7
F=1		 3·5·7
F=2		 3·5·7
F=22

     2·3·5·7
F=1		 2·3·5·7
F=2		 2·3·5·7
F=22		 2·3·5·7
F=23		  
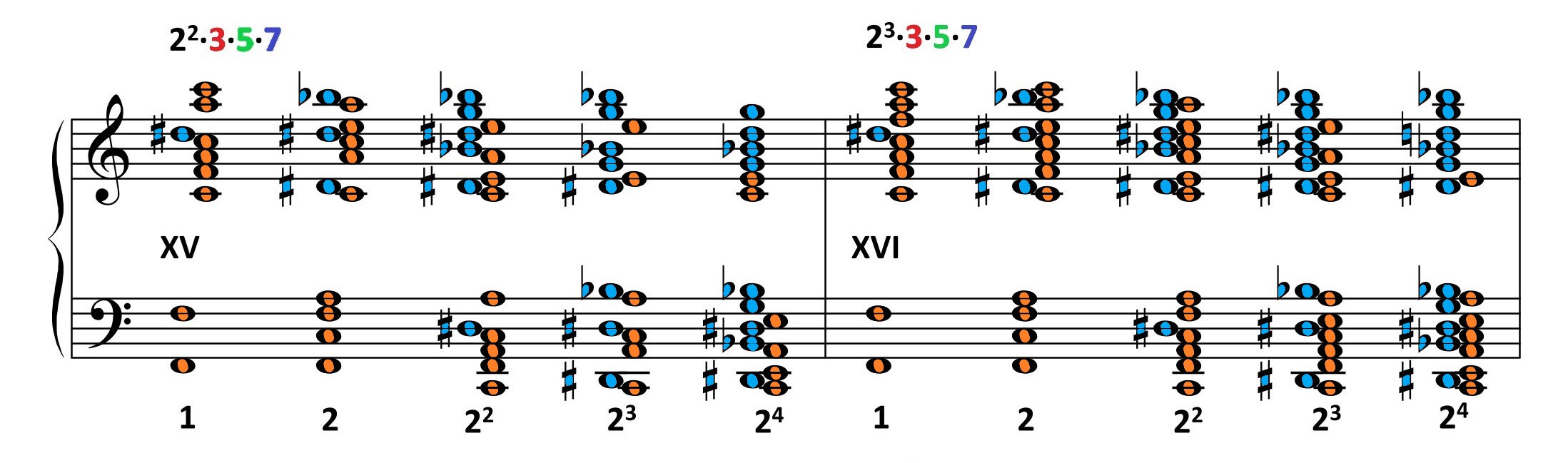
22·3·5·7
F=1		 22·3·5·7
F=2		 22·3·5·7
F=22		 22·3·5·7
F=23		 22·3·5·7
F=24		   23·3·5·7
F=1		 23·3·5·7
F=2		 23·3·5·7
F=22		 23·3·5·7
F=23		 23·3·5·7
F=24

 

species VI*
Konsonanzen Homepage species VI 7

52·7
F=1

 52·7
F=2		 52·7
F=22		 52·7
F=23		 52·7
F=24 		   2·52·7
F=1		 2·52·7
F=2		 2·52·7
F=22		 2·52·7
F=23		 2·33·7
F=24 
22·52·7
F=1

 22·52·7
F=2		 22·52·7
F=22		 22·52·7
F=23		 22·52·7
F=24		   23·52·7
F=1		 23·52·7
F=2		 23·52·7
F=22		 23·52·7
F=23		 23·52·7
F=24
  24·52·7
F=1		   24·52·7
F=2		   24·52·7
F=22		   24·52·7
F=23		   24·52·7
F=24		  

 

species VII*
Konsonanzen Homepage species VII7

33·7
F=1

 33·7 
F=2		 33·7 
F=22		 33·7 
F=23		 33·7 
F=24 		   2·33·7 
F=1		 2·33·7 
F=2		 2·33·7 
F=22		 2·33·7 
F=23		 2·33·7
F=24 
22·33·7 
F=1		 22·33·7 
F=2		 22·33·7 
F=22		 22·33·7 
F=23		 22·33·7 
F=24		   23·33·7 
F=1		 23·33·7 
F=2		 23·33·7 
F=22		 23·33·7 
F=23		 23·33·7 
F=24

 

species VIII*
Konsonanzen Homepage species VIII7

32·5·7
F=1

 32·5·7
F=2		 32·5·7
F=22		 32·5·7
F=23		 32·5·7
F=24 		   2· 32·5·7
F=1		 2· 32·5·7
F=2		 2· 32·5·7
F=22		 2· 32·5·7
F=23		 2· 32·5·7
F=24 
22·32·5·7
F=1		   22·32·5·7 
F=2		   22·32·5·7 
F=22		   23·32·5·7
F=1		   23·32·5·7 
F=2		   23·32·5·7 
F=22

 

species IX*
Konsonanzen Homepage species IX7



 3·52·7
F=1
 3·52·7
F=2

3·52·7
F=22

 3·52·7 
F=23		 2·3·52·7 
F=1		 2·3·52·7
F=2		 2·3·52·7
F=22		 2·3·52·7
F=23
22·3·52·7
F=1 		   22·3·52·7
F=2		   22·3·52·7
F=22		   22·3·52·7
F=23

 

species X*
Konsonanzen Homepage species X7



 33·5·7
F=1		 33·5·7
F=2

33·5·7
F=22

 33·5·7
F=23		 2·33·5·7
F=1		 2·33·5·7
F=2		 2·33·5·7
F=22		 2·33·5·7
F=23
22·33·5·7
F=1		 22·33·5·7
F=2		 22·33·5·7
F=22		 23·33·5·7
F=1		 23·33·5·7
F=2		 23·33·5·7
F=22 

 

species XI*
Konsonanzen Homepage species XI7

 

32·52·7
F=1

 32·52·7
F=2		 32·52·7
F=22		 2·32·52·7
F=1
 2·32·52·7
F=2
 2·32·52·7
F=22
  22·32·52·7
F=1
   22·32·52·7
F=2
   22·32·52·7
F=22

 

species XII*Konsonanzen Homepage species XII7

 

33·52·7
F=1

 33·52·7
F=2		 33·52·7
F=22		 2·33·52·7
F=1
 2·33·52·7
F=2
 2·33·52·7
F=22
  22·33·52·7
F=1
   22·33·52·7
F=2
   22·33·52·7
F=22