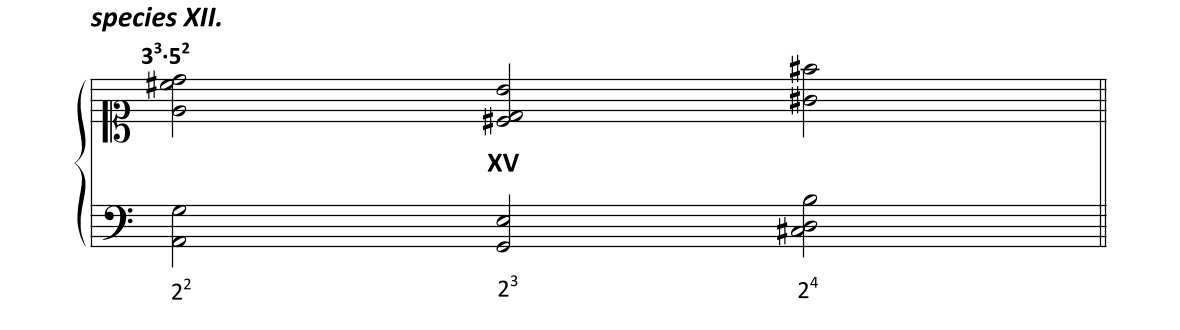genus musicum diatonico-chromaticum

 genus musicum XVIII.       exponens 2m·33·52
   F  Fs  G  Gs  A  B   H  c  cs  d  ds  e  f
29 22·33·5 26·32 23·3·52 27·5 20·33·52 24·32·5 28·3 25·52 25·33 22·32·52 26·3·5 210
512 540 576 600 640 675 720 768 800 864 900 960 1024
 f 210 1024  1/2  135/256  9/16  75/128  5/8  675/1024  45/64  3/4  25/32  27/32  225/256  15/16  1
 e 26·3·5 960  8/15  9/16  3/5  5/8  2/3  45/64  3/4  4/5  5/6  9/10  15/16  1  16/15
 ds 22·32·52 900  128/225  3/5  16/25  2/3  32/45  3/4  4/5  64/75  8/9  24/25  1  16/15  256/225
 d 25·33 864  16/27  5/8  2/3  25/36  20/27  25/32  5/6  8/9  25/27  1  25/24  10/9  32/27
 cs 25·52 800  16/25  27/40  18/25  3/4  4/5  27/32  9/10  24/25  1  27/25  9/8  6/5  32/25
 c 28·3 768  2/3  45/64  3/4  25/32  5/6 225/256  15/16  1  25/24  9/8  75/64  5/4  4/3
 H 24·32·5 720  32/45  3/4  4/5  5/6  8/9  15/16  1  16/15  10/9  6/5  5/4  4/3  64/45
 B 20·33·52 675  512/675  4/5  64/75  8/9  128/135  1  16/15  256/225  32/27  32/25  4/3  64/45  1024/675
 A 27·5 640  4/5  27/32  9/10  15/16  1  135/128  9/8  6/5  5/4  27/20  45/32  3/2  8/5
 Gs 23·3·52 600  64/75 9/10  24/25  1  16/15  9/8  6/5  32/25  4/3  36/25  3/2  8/5  128/75
 G 26·32 576  8/9  15/16  1  25/24  10/9  75/64  5/4  4/3  25/18  3/2  25/16  5/3  16/9
 Fs 22·33·5 540  128/135  1  16/15  10/9  32/27  5/4  4/3  64/45  40/27  8/5  5/3  16/9  256/135
 F 29 512  1  135/128  9/8  75/64  5/4  675/512  45/32  3/2  25/16  27/16  225/128  15/8  2

 

Dieses Tongeschlecht besteht aus 12 Tönen. Die Abstände von aufeinander folgenden Tönen sind darin alle ähnlich groß.

Graphische logarithmische Darstellung des XVIII. Tongeschlechts:

18 

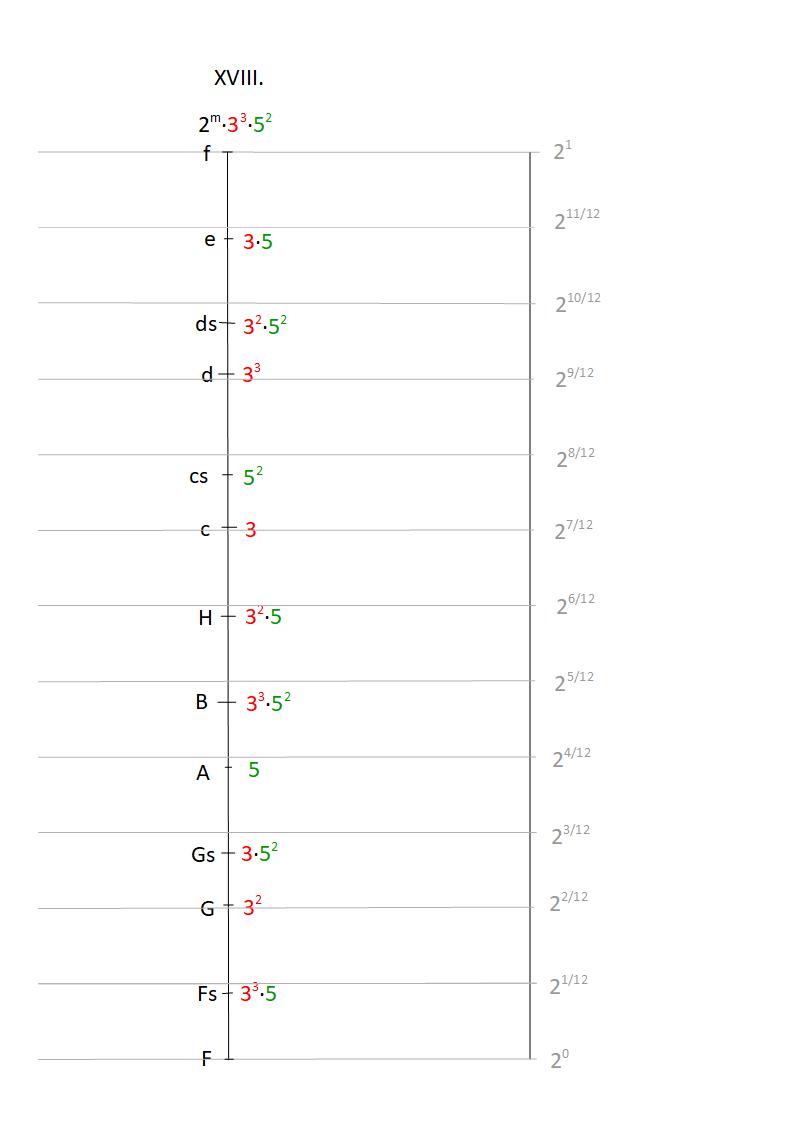
Konsonanzen im diatonisch-chromatischen Geschlecht:

Die Darstellungszahl (exponens) einer Konsonanz wird nach Leonhard Euler durch das kleinste gemeinsame Vielfache der Einzeltöne (=deren Zahlen) gefunden. Umgekehrt kann man aus einer gegebenen Darstellungszahl zugehörige Konsonanzen durch Bestimmen aller Teiler finden. 
Im diatonisch-chromatischen Geschlecht mit exponens 2m·33·52 listet Euler daher folgende 12 species von Konsonanzen auf:

species I. 2m
species II. 2m·3
species III. 2m·5
species IV. 2m·32
species V. 2m·3·5
species VI. 2m·52
species VII. 2m·33
species VIII. 2m·32·5
species IX. 2m·3·52
species X. 2m·33·5
species XI. 2m·32·52
species XII. 2m·33·52

 

Jeder Darstellungszahl (exponens) kann nach Euler ein Grad der Annehmlichkeit (gradus suavitatis) durch folgende Vorschrift zugeordnet werden:
GS(E) = (Summe aller Primteiler von E) – (Anzahl aller Primteiler von E) + 1
oder GS(E) = Σ(pk – 1)·nk + 1  , wenn der exponens die eindeutige Primfaktorzerlegung E = Πpknk besitzt,
oder induktiv: GS(p) = p, wenn p Primzahl, GS(a·b) = GS(a) + GS(b) – 1

Je kleiner der gradus suavitatis einer Konsonanz ist, desto einfacher kann sie wahrgenommenwerden, höhere gradus ergeben sich bei komplexeren Konsonanzen.

So erhält man für die oben aufgelisteten Konsonanzen folgende Grade:

gradus suavitatis I II III IV V VI VII VIII IX X XI XII XIII XIV XV
species I.  1   2  22                        
species II.     3 2·3 22·3 23·3                  
species III.         5 2·5 22·5 23·5 24·5            
species IV.          32 2·32 22·32 23·32 24·32 25·32          
species V.             3·5 2·3·5 22·3·5 23·3·5 24·3·5 25·3·5      
species VI.                  52  2·52  22·52  23·52  24·52  25·52  26·52
species VII.              33  2·33  22·33  23·33  24·33  25·33  26·33    
species VIII.                  32·5 2·32·5  22·32·5  23·32·5  24·32·5  25·32·5  26·32·5
species IX.                       3·52  2·3·52  22·3·52  23·3·52  24·3·52
species X.                      33·5  2·33·5  22·33·5  23·33·5  24·33·5
species XI.                          32·52  2·32·52  22·32·52
species XII.                              33·52

Leonhard Euler notiert in Folge obige Konsonanzen in zwei Fünfliniensystemen (eines im Bass-, eines im Diskantschlüssel).
Untere Grenze ist das F, obere das f". Für die Basis F nimmt Euler entweder die 1 oder eine Potenz der 2 an.

2m
Konsonanzen Homepage Species1 1

2m·3
Konsonanzen Homepage Species2 1

2m·5
Konsonanzen Homepage Species3 1

2m·32
Konsonanzen Homepage Species4 1

2m·3·5
Konsonanzen Homepage Species5 1

2m·52
Konsonanzen Homepage Species6 1

2m·33
Konsonanzen Homepage Species7 1

2m·32·5
Konsonanzen Homepage Species8 1

2m·3·52
Konsonanzen Homepage Species9 1

2m·33·5
Konsonanzen Homepage Species10 1

2m·32·52Konsonanzen Homepage Species11 1

2m·33·52
Konsonanzen Homepage Species12 1

 

  I II III IV V  VI  VII   VIII   IX    X    XI     XII      XIII     XIV      XV       
sp. I. 1
F=1		 2
F=1		 22
F=1		                                                       
sp. II.     3
F=1		 2·3
F=1		 22·3
F=1		 22·3
F=2		 23·3
F=2		                                                 
sp. III.         5
F=1		 2·5
F=1		 2·5
F=2		 22·5
F=1		 22·5
F=2		 22·5
F=22		 23·5
F=2		 23·5
F=22		 24·5
F=22		                                     
sp. IV.          32 2·32
F=2 		 22·32
F=2		 22·32
F=22		 23·32
F=2		 23·32
F=22		 23·32
F=23		 24·32
F=22		 24·32
F=23		 25·32
F=23		                                 
sp. V.             3·5
F=1		 3·5
F=2		 2·3·5
F=1		 2·3·5
F=2		 2·3·5
F=22		 22·3·5
F=2		 22·3·5
F=22		 22·3·5
F=23		 23·3·5
F=2		 23·3·5
F=22		 23·3·5
F=23		 24·3·5
F=22		 24·3·5
F=23		 25·3·5
F=23		                      
sp. VI.                 52 2·52 22·52
F=22		 23·52
F=22		 23·52
F=23		 24·52
F=22		 24·52
F=23		 24·52
F=24		 25·52
F=23		 25·52
F=24		 26·52
F=24		  
sp. VII.             33 2·33  22·33
F=22		 23·33
F=22		 23·33 
F=23		 24·33
F=22		 24·33
F=23		 24·33
F=24		 25·33
F=23		 25·33
F=24		 26·33
F=24		      
sp. VIII.                 32·5
F=2		 2·32·5
F=2		  2·32·5
F=22		 2·32·5
F=23		 22·32·5
F=2 		  22·32·5
F=22		 22·32·5
F=23		 22·32·5
F=24 		 23·32·5
F=2		 23·32·5
F=22		 23·32·5
F=23		 23·32·5
F=24		 23·32·5
F=25		 24·32·5
F=22		 24·32·5
F=23		 24·32·5
F=24		 24·32·5
F=25		 25·32·5
F=23		 25·32·5
F=24		 25·32·5
F=25		 26·32·5
F=24		 26·32·5
F=25 
sp. IX.                     3·52 2·3·52
F=22		 22·3·52
F=22		 22·3·52
F=23		 23·3·52
F=22		 23·3·52
F=23		 24·3·52
F=22		 24·3·52
F=23		 24·3·52
F=24		 24·3·52
F=25		    
sp. X.                     33·5
F=22 		 2·33·5
F=22		 2·33·5 
F=23		 22·33·5
F=22		 22·33·5
F=23		 22·33·5
F=24		 23·33·5
F=22		 23·33·5
F=23		 23·33·5
F=24		 23·33·5
F=25		 24·33·5
F=22		 24·33·5
F=23		 24·33·5
F=24		 24·33·5
F=25		 24·33·5
F=26		    
sp. XI.                         32·52
F=22		 32·52 
F=23 		 2·32·52
F=22		 2·32·52
F=23		 2·32·52
F=24		 22·32·52
F=22		 22·32·52
F=23		 22·32·52
F=24		 22·32·52
F=25		    
sp. XII.                           33·52
F=22		 33·52
F=23		 33·52
F=24